Given an array of 'N' numbers consisting only 0's, 1's and 2's in random order. Our work is to segregate the integers in such a way that the resultant array should be in sorted order (i.e) 0's are in one side, 1's are in the middle and 2's are segregated together at the end of the array. We should sort this array in O(N) time complexity.
Yes. We can easily solve this problem by calling in-built sort function(This doesn't take O(N)) or
implement any of the appropriate sorting methods.
Also, we know that the best sorting methods like merge sort, quick sort and heap sort takes
O(N log N) in the best case scenario.
Is there an efficient sorting algorithm to sort an array in O(N) time complexity?
The answer is No.
Yes. Counting 0's, 1's, 2's and then filling the array in that order with respect to the count will give the sorted array in the time complexity of O(2*N), this is because we are traversing the array twice, one for counting and another for filling. This is not so efficient, Although O(2*N) = O(N) in asymptotic analysis.
Here comes the Dutch National Flag algorithm to solve this problem in O(N) time complexity.
This algorithm is proposed by the famous Dutch Computer Scientist Edsger Wybe Dijkstra
This algorithm is named after the Dutch flag as it contains three colours red, white and blue.
We will have three integers to have a track on the integers of the array. They are Low, Mid and High.
1. Low points at the beginning of the array and have a track of 0's.
2. Mid traverses through the entire array.
3. High points at the end of the array and have a track of 2's.
As we traverse through the array,
If mid encounters 0, swap a[low] and a[mid](as low tracks of 0's) and then increment low and mid. As a result of this 0's will be segregated in one side.
If mid encounters 1, No swapping is needed. We have to increment mid.
If mid encounters 2, swap a[mid] and a[high],(as high tracks of 2's) and then we decrement high.
We are not incrementing mid in Case 2. This is because if a[mid] = 2 and a[high] = 0, we swap 2 and 0. Now mid points to 0 and we have to bring back 0 to its position by swapping 0 with a[low].
If we have incremented mid, we would not have swapped 0 and a[low]. Hence we don't increment mid in case 2.
Finally, Our array will have 0's, 1's and 2's in sorted order.
This algorithm works with all arrays consisting of only three values.
There are many ways to solve this problem. We can do
SORTING
Yes. We can easily solve this problem by calling in-built sort function(This doesn't take O(N)) or
sort( array-name, array-name + size_of_array );
Also, we know that the best sorting methods like merge sort, quick sort and heap sort takes
O(N log N) in the best case scenario.
Is there an efficient sorting algorithm to sort an array in O(N) time complexity?
The answer is No.
COUNTING THE INTEGERS
Yes. Counting 0's, 1's, 2's and then filling the array in that order with respect to the count will give the sorted array in the time complexity of O(2*N), this is because we are traversing the array twice, one for counting and another for filling. This is not so efficient, Although O(2*N) = O(N) in asymptotic analysis.
Here comes the Dutch National Flag algorithm to solve this problem in O(N) time complexity.
DUTCH NATIONAL FLAG ALGORITHM
This algorithm is proposed by the famous Dutch Computer Scientist Edsger Wybe Dijkstra
This algorithm is named after the Dutch flag as it contains three colours red, white and blue.
Explanation:
We will have three integers to have a track on the integers of the array. They are Low, Mid and High.
1. Low points at the beginning of the array and have a track of 0's.
2. Mid traverses through the entire array.
3. High points at the end of the array and have a track of 2's.
As we traverse through the array,
If mid encounters 0, swap a[low] and a[mid](as low tracks of 0's) and then increment low and mid. As a result of this 0's will be segregated in one side.
If mid encounters 1, No swapping is needed. We have to increment mid.
If mid encounters 2, swap a[mid] and a[high],(as high tracks of 2's) and then we decrement high.
We are not incrementing mid in Case 2. This is because if a[mid] = 2 and a[high] = 0, we swap 2 and 0. Now mid points to 0 and we have to bring back 0 to its position by swapping 0 with a[low].
If we have incremented mid, we would not have swapped 0 and a[low]. Hence we don't increment mid in case 2.
Finally, Our array will have 0's, 1's and 2's in sorted order.
This algorithm works with all arrays consisting of only three values.
Source Code:
#include<bits/stdc++.h>
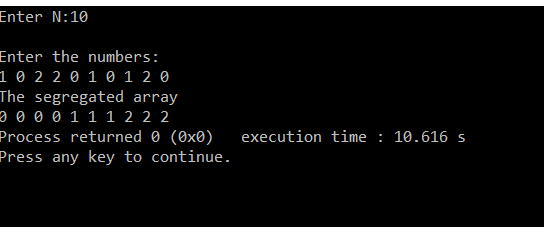
Output:
Cleanly written.Kudos.
ReplyDeleteSuper da 👍
ReplyDeleteThank you Kawin
Delete